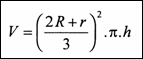13. Volumen als Grenzwert
ARCHIMEDES konnte das Volumen der Kugel&xnbsp; auch mit einer anderen Methode&xnbsp; bestimmen - mit der sogenannten EXHAUSTIONSMETHODE:
Wir stellen uns wieder eine Halbkugel vor. diese zerteilen wir durch Zerschneiden parallel zur Begrenzungsfläche in n gleich dicke Teile. Diese Teile ersetzen wir durch Zylinderscheiben. Deren Volumen lässt sich berechnen und wir erhalten eine Näherung für das Maß des Kugelvolumens.
| |
n Teile; Höhe einer Scheibe: Radius der i-ten Scheibe: Volumen der i-ten Scheibe: Summe aller Scheibenvolumina: |
Durch Erhöhung der Anzahl der Scheiben wird diese Näherung immer genauer, in der Grenze für n® ¥ (Schichtendicke ® 0) erhalten wir das Kugelvolumen.
&xnbsp;&xnbsp; ![]()
Die verwendete Methode lässt sich auf die Berechnung anderer Körpervolumina anwenden:
| |
Bei Kenntnis der Querschnittsfunktion kann der Grenzwert dann konkret berechnet werden! |
Die Summe aller Querschnittsflächen führt zum Integralbegriff. Ein genaueres Eingehen darauf würde den Rahmen dieser Vorlesung sprengen.

Wichtige Begriffe:&xnbsp;&xnbsp; .......... Spundloch,&xnbsp;&xnbsp; ............ Dauben
| KEPLER, 1613 („Stereometria doliorum vinariorum“
„Die Stereometrie der Weinfässer“) betrachtete Fässer mit verschiedenen
Daubenformen (parabel-, ellipsen- und hyperbelförmige Dauben). Ausgangspunkt
seiner Arbeit war die Überprüfung der damals gängigen Methode zur
Inhaltsbestimmung mit Hilfe eines Meßstabes. Die nebenstehende Skizze
wurde aus [KARLSON, Du und der Zauber der Zahlen, 1954] entnommen. |
|
|
|
|
| SIMPSONsche Regel, 18. Jahrhundert |
LAMBERT, 1765 |
[1] Aus&xnbsp; [DAINTITH 1989]