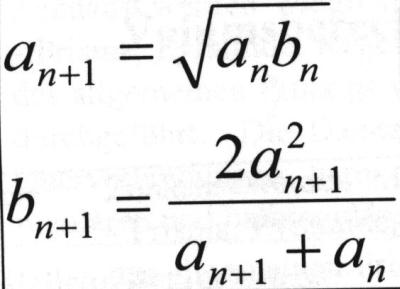Zur Übersicht

9.&xnbsp;Kreisformeln

Berechnungen von Kreisumfang und Kreisfläche sind untrennbar&xnbsp; mit dem Mathematiker ARCHIMEDES (287 - 212 v.Chr. SYRAKUS, „Störe meine Kreise nicht“) verbunden.

A) Kreisumfang

Der Umfang wird durch ein-und umgeschriebene Polygone angenähert, z.B. durch ein reguläres Sechseck und ein Quadrat:

6.r&xnbsp; £ u £&xnbsp; 8.r&xnbsp;&xnbsp;&xnbsp; (2.r = d)

Kreisumfang =

Durchmesser mal einer Zahl zwischen 3 und 4.

ARCHIMEDES führte dieses Verfahren bis zum ein-und umgeschriebenen 96-eck durch und erhielt:

Erst später wurde durch Leonhard EULER (1707 - 1783) diese Verhältniszahl durch p abgekürzt:

p= 3, 14159 26535 89793 23846 ...

Leonhard EULER auf dem
10-Franken-Schein

Verschiedene Merkverse erleichterten früher das Behalten der ersten Stellen dieser irrationalen Dezimalzahl, wie zum Beispiel:

Wie

,

o

dies

p

macht

ernstlich

so

vielen

viele

  

3

,

1

4

1

5

9

2

6

5

3

Für FreundINNEN utopischer Romane sei auf den Roman „CONTACT“ von Carl SAGAN (KNAUR Bd.1680) hingewiesen, in dem diese transzendente Zahl eine gewisse Rolle spielt! (Verfilmung 1997)

B)&xnbsp;Kreisfläche

Man nähert die Kreisfläche durch die Inhalte ein-und umgeschriebender Vielecke an:

n.As&xnbsp; £ A £&xnbsp; n.AS&xnbsp;

Im Grenzübergang von n gegen ¥ ergibt sich:

In der Schule bewährt sich ein anderes Verfahren zur Herleitung der Flächenformel, wenn der Umfang bereits bekannt ist:&xnbsp; Die Kreisscheibe wird in gleich große Sektoren zerteilt, diese werden dann anders angeordnet.

Kreisflaechenherleitung in der Schule

C) Kreisteile

Sektor(Ausschnitt)

Segment (Abschnitt)

Beispiel: Inhalt einer „Linse“

Der Vollständigkeit halber seien noch die Formeln für die Berechnung des Flächeninhaltes einer Ellipse angegeben:

 

A&xnbsp; =

D)&xnbsp;Der Kreis und das isoperimetrische Problem

Experiment: In einem Drahtrahmen wird eine Schinge aus einem Seidenfaden lose befestigt, der Rahmen in eine Seifenlösung getaucht: Eine Seifenhaut bildet sich im Rahmen, der den Faden trägt. Das Innere der Fadenschlinge wird durch eine „Platzenlassen“ von der Seifenhaut befreit. Blitzartig springt die dann Fadenschlinge auf eine kreisförmige Schlinge um. Durch die Oberflächenspannung&xnbsp; der Seifenhaut bildet diese eine möglichst kleine Oberfläche. Nach Zerstörung der Seifenhaut im Inneren&xnbsp; bildet die Haut zwischen Faden und Drahtrahmen eine möglichst kleine Oberfläche, die Fläche im Inneren des Fadenringes wird demnach möglichst groß.

Damit wurde der physikalische Beweis für die Lösung des isoperimetrischen Problemes („iso“...gleich, „perimeter“...Umfang) erbracht.

Unter allen Figuren mit gleichem Umfang ist diejenige zu finden, die größten Flächeninhalt hat.

(Vgl. Sage von Königin DIDO bei der Gründung KARTHAGOS)

Mathematisch lässt sich die Lösung des Problems etwa folgendermaßen einsehen:

[Nach Jakob STEINER, 1796 - 1863, BERN, BERLIN; Autodidakt), eine Beweislücke wurde von Karl WEIERSTRASS (1815 - 1897, BERLIN; „Ein Mathematiker, der nicht etwas POET ist, wird nie ein vollkommener Mathematiker sein“) geschlossen]:


Anmerkung: In der Ebene gilt die isoperimetrische Ungleichung&xnbsp;&xnbsp;


E) Berechnung von PI &xnbsp;mit einer Rekursion:

Auf derartige Formeln kommt man in Anlehnung auf die Herleitung der Zahl p mit Hilfe ein- und umge-schriebener Vielecke.

Als Startwerte könnte man etwa für ao = 2 und bo = 4 wählen ....

Eine Auflistung könnte etwa mit Hilfe einer&xnbsp; Tabellenkalkulation erfolgen.

Auch viele Reihen haben als Grenzwert die Zahl p oder einen Teiler davon, z.B.:





F) Ergänzungen aus [VORDERMAN 1996]

&xnbsp;


[1] Ingrid LEWISCH:&xnbsp; Mathematics – Special topics for the 4th class, R. Oldenbourg Verlag Wien , 1996
Zum Inhaltsverzeichnis