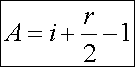6.&xnbsp;&xnbsp;&xnbsp;&xnbsp; Zerlegungsgleichheit, Scherung

Zwei grundsätzliche Sätze für die Flächenberechnung:

A)&xnbsp; Kongruente Figuren haben denselben Flächeninhalt.







B) Können zwei Figuren in paarweise gleiche Teilfiguren zerlegt werden, so haben sie denselben Flächeninhalt. Solche Figuren heißen „zerlegungsgleich“.

 








Beispiel: Figuren aus den 7 TANGRAM-Teilen (vgl. EG 1) sind immer&xnbsp; flächengleich, da sie zerlegungsgleich sind!













Flächeninhalt eines Parallelogramms

Die Herleitung folgt unmittelbar oben angegebenen Axiomen.

Durch eine Diagonale wird ein Parallelogramm in zwei kongruente Dreiecke geteilt (Kongruenz-satz:..............).&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp; Daraus folgt:
















Flächeninhalt eines Dreiecks

&xnbsp;A =













Scherung - eine flächeninhaltserhaltende Abbildung

Der Flächeninhalt bleibt gegenüber allen Kongruenz-abbildungen invariant (folgt aus ......),&xnbsp; gegenüber allen anderen Abbildungen (Ähnlichkeits- und affinen Abbildungen) im allgemeinen nicht.

Bei einer speziellen Affinität (siehe auch EG I/Affinität), der Scherung, besteht doch eine Invarianz des Flächeninhalts.

Angabe einer Scherung erfolgt&xnbsp; durch

...... Affinitätsachse (Fixachse)&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp; .......Punktepaar&xnbsp;

Die Konstruktion der Bildfigur benützt hauptsächlich die Geradentreue und die Fixpunkte!

Warum ist die Scherung flächentreu?

Antwort:

1. Schritt:

Dreiecke, von denen eine Seite in der Scherungsachse liegt, bleiben nach der Abbildung&xnbsp; flächengleich.

2. Schritt:

Dreiecke mit einer Seite parallel zur Scherungsachse bleiben ebenso flächen-gleich.

3. Schritt:

Dreiecke mit Seiten allgemeiner Lage zur Scherungsachse bleiben&xnbsp; flächen-gleich.

4. Schritt:

Allgemeine Vielecke und andere Figuren bleiben flächengleich.

Anwendung der Scherung - Eckenabschneiden

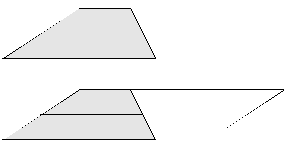
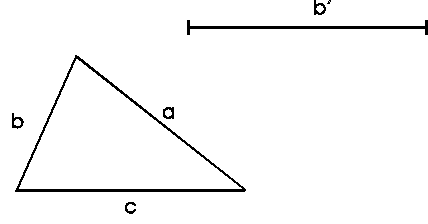
  • Ein gegebenes Dreieck soll in ein flächengleiches Dreieck mit gegebener Seitelänge&xnbsp; b’ verwandelt werden.

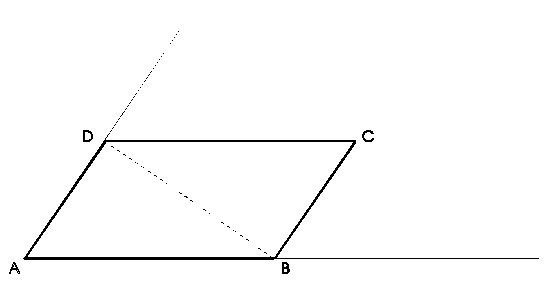
  • Ein Viereck (z.B. Parallelogramm) soll durch Eckenabschneiden in ein flächengleiches Dreieck verwandelt werden:

  • Durch Eckenabschneiden lässt sich jedes n-eck in ein flächengleiches n-1-Eck (und somit sukzessive in ein Dreieck verwandlen)











7.&xnbsp;&xnbsp;&xnbsp;&xnbsp; Flächenberechnungen

A) Eine Ergänzung zu den Dreiecksflächenformeln

Nur aus der Kenntnis der drei Seitenlängen eines Dreiecks lässt sich der Flächeninhalt eines Dreiecks mit der sogennannten HERONschen Formel berechnen [HERON, um 130 n.Chr., Alexandria; Formel stammt allerdings von ARCHIMEDES]

&xnbsp;

wobei s&xnbsp; gleich dem halben Umfang ist. (Herleitung siehe etwa WITTMANN 1987,&xnbsp; Seite 374)









B) Herleitung wichtiger elementarer Formeln

Bekannt:
Quadrat, Rechteck, Dreieck, Parallelogramm

Eine mögliche Herleitung des Trapezinhaltes:







C)&xnbsp; Flächeninhaltsberechnungen allgemeiner Vier- und Vielecke

Eckenabschneiden: (theoretische Methode) Durch Eckenabschneiden wird die Figur in ein flächengleiches Dreieck verwandelt, von dem mit der Formel der Inhalt berechnet werden kann.


Dreieckszerlegungsmethode:Durch Diagonalen zerlegt man das Vieleck in Dreiecke

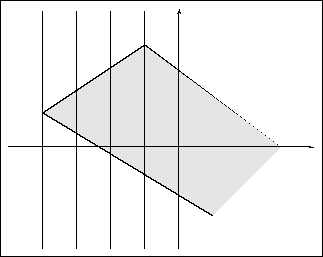
Standlinienmethode („Trapezmethode“)

Nach der Wahl einer beliebígen Geraden (Straßenkante) als Standlinie&xnbsp; misst man den Abstand jedes Eckpunktes von dieser Geraden. Es entstehen Trapeze (allenfalls Dreiecke, falls die Standlinie durch einen Eckpunkt geht!)

 

 

Koordinatensystemmethode

Am besten umschreibt man ein Rechteck und zieht entstehende Inhalte von Dreiecken und Trapezen ab.





Ohne Beweis werden nun zwei weitere Möglichkeiten der Flächenberechung angeboten:

Formel von PICK

Man zählt die Gitterpunkte und schließt dann mit der Formal auf den Flächeninhalt.

(Georg PICK, Prag, 1942 im KZ gestorben)

Wichtige Folgerung: Lässt man nur ganzzahlige Angabekoordinaten zu, dann ist der Flächeninhalt auch ganzzahlig oder hat höchstens die Zehnteldezimalstelle 5.






Formel von GAUSS

&xnbsp;(CARL FRIEDRICH GAUSS, 1777 - 1855 , „Princeps mathematicorum“)

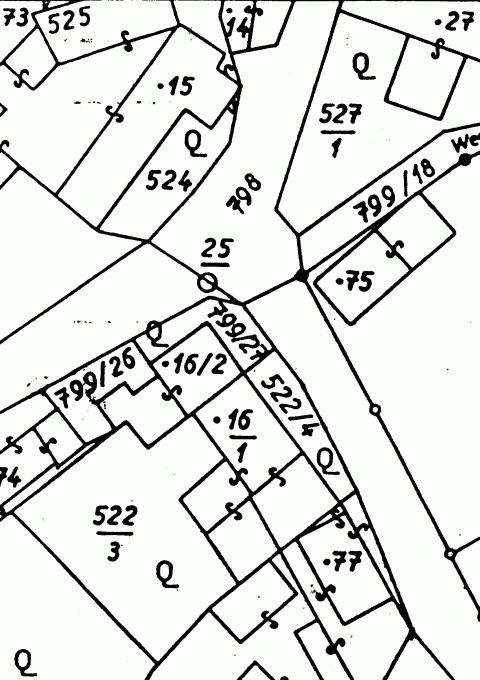
Verwendung v.a. im Vermessungswesen: Berechnung von Grundstücksflächeninhalten

P(xi/yi)&xnbsp; seien die Koordinaten der Eckpunkte (i = 1, 2, 3, 4, ...)

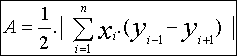
Beispiel: P1(3/0), P2(-1/3),
              P3(-4/1), P4(1/-2)

Aus der Katastralmappe:


Zum Inhaltsverzeichnis